註：本文同步更新在Notion!（數學公式會比較好閱讀）

行列式 (Determinant)

行列式是矩陣中的一個重要概念，通常用於判斷矩陣是否可逆。如果矩陣的行列式不為零，那麼這個矩陣是可逆的，這在線性代數和機器學習中有著廣泛的應用。例如，在解線性方程組時，若係數矩陣的行列式為零，則無法唯一解出結果。

行列式的計算

行列式的應用包括矩陣可逆性檢查、矩陣特徵值與特徵向量的計算、以及線性變換的縮放因子等。

向量範數 (Vector Norm)

範數是用來度量向量大小的工具。在機器學習中，範數的概念非常重要，尤其是在優化問題中，範數可以用來約束或正則化模型。例如，在 Lasso 和 Ridge 回歸中，分別使用了L1 和 L2 範數來進行正則化。

常見的範數有：

• L1 範數：即向量的元素絕對值之和。
  
• L2 範數：即向量元素平方和的平方根。
  
• L_\infty 範數：即向量中元素的最大值。
  

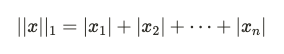
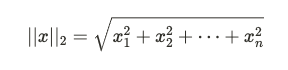
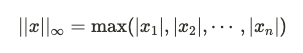
範數對於衡量向量距離、正則化以及梯度下降算法中的步長調整都具有重要意義。

內積 外積 元素積

內積 (Dot Product)

內積是一種常用的向量運算，特別是在機器學習和向量空間中，它可以用來衡量兩個向量之間的相似度。給定兩個向量 a 和 b，它們的內積定義為：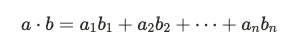

如果兩個向量的內積為零，則說明它們是正交的（即互相垂直）。在神經網絡中，內積是計算每層加權輸入的核心運算。

外積 (Cross Product)

外積僅在三維空間中定義，結果是一個與兩個向量都垂直的向量。給定兩個三維向量 a 和 b ，它們的外積定義為：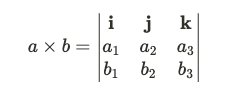

外積在計算向量間的面積、平行四邊形面積和物理學中的力矩運算中具有應用。

元素積 (Hadamard Product)

元素積是矩陣中每一個元素對應相乘的操作，對於機器學習中的卷積神經網絡（CNN）或其他點對點操作中非常有用。給定兩個矩陣 A 和 B：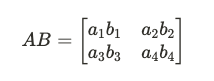

擬反矩陣

擬反矩陣，也稱為 Moore-Penrose 逆矩陣，是一種用來處理無法直接求逆的矩陣的技術。當矩陣不滿足可逆條件時（例如行列式為零），可以使用擬反矩陣來找到一個“最佳解”。

擬反矩陣特別適合處理過定和欠定系統，可以通過奇異值分解（SVD）來計算。

特徵向量(Eigenvectors)

特徵向量與特徵值是線性代數中的核心概念，尤其是在主成分分析（PCA）和共變異數矩陣的分解中。
簡單來說，

PCA 通常用來降維，將高維數據轉換為較低維數據，同時保留數據中最多的變異性。這是通過對共變異數矩陣進行特徵分解，保留最大特徵值對應的特徵向量來實現的。

理解行列式、範數、內積與外積、特徵向量及擬反矩陣這些線性代數中的核心概念，對於深入機器學習和數據科學非常關鍵。這些數學工具構成了機器學習算法的基礎，使我們能夠更有效地處理高維數據、進行降維和優化模型。

所以別放棄啊，各位！

比眼下這個情況還複雜的，恐怕只有三角函數了。
//
推薦給各位一個很有趣的迷因網站！點我